Independent study at UCSD

Year: January–June 2015

Technology: Matlab, Overleaf

Description

Independent study at UCSD, 2 quarters. Write a paper with Professor James friend called “An investigation of maximum particle velocity as a universal invariant—Defined by a statistical measure of failure or plastic energy loss for acoustofluidics applications”

Problem statement

I first joined Professor Friend’s lab in 2017, right after I took his class on advanced analytical methods for solving non-linear ODEs using MATLAB. I was the only undergraduate in his lab, so there was a limited number of projects he could assign me due to my limited expertise.

Over the years, Professor Friend noticed a trend across his experiments, which typically dealt with vibrations through robotics that happened at high frequencies. What he discovered was that if you solve for the maximum particle velocity inside a vibration wave in a solid (typically longitudinal but also can be transverse or shear waves), it never exceeds 1 meter per second regardless of the frequency of vibration. We believed this to be a fundamental property in nature, regardless of the material properties of the solid that is vibrating.

My role

Professor Friend and I dug into some of the fundamental equations that might be driving this effect, and we discovered there is a theoretical velocity limit for each material in which it will experience cyclical yield stress and will inevitably “fail” and break. We called this theoretical limit “v_max”, as it was a unique material property that could be calculated as shown below.

Solving for v_max as a function of yield stress (σ_y), elastic modulus, (E) and density (ρ) (equation shown to the right)

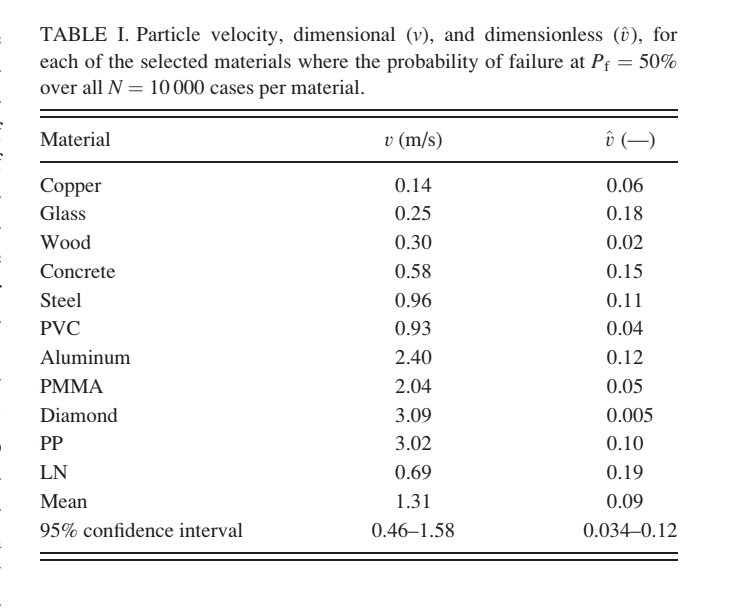
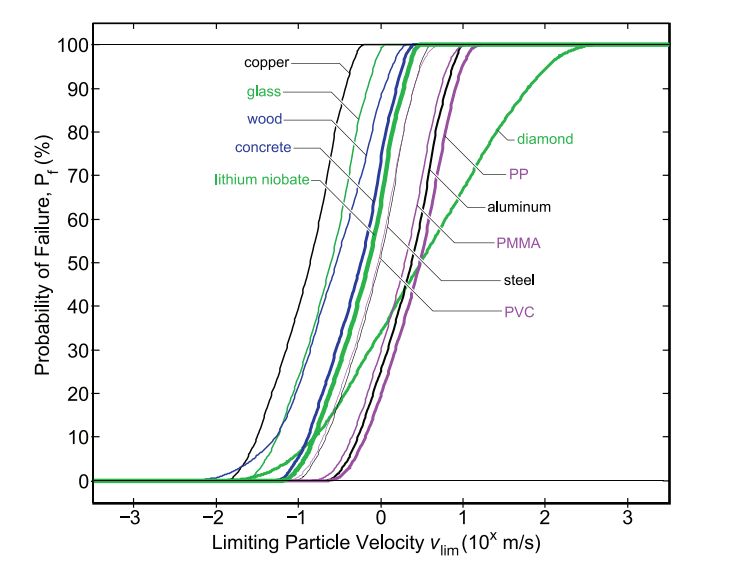
To determine the range of v_max values in nature (in meters per second), we settled on 11 materials that range all over the spectrum of solids (metals, plastics, rubbers, etc. —wood, diamond, copper, PVC, PMMA, steel, aluminum, polypropylene, concrete, glass, lithium niobate (a synthetic salt))— and calculated their v_max values. Unsurprisingly, most v_max values ranged from 0.1 to 10 meters per second, with diamond being at 100 meters per second due to its unique material properties (high yield stress relative to density and elastic modulus). However, we concluded that because v_max is an ideal interpretation of the velocity limit, real life material samples often have imperfections that can cause stress concentrations and induce crack propagation or material failure well before the particle velocity reaches v_max.

To address the effects of these imperfections on each sample’s theoretical maximum particle velocity, we assigned factors in reducing maximum particle velocity (“psi” (Ψ)), and used Monte Carlo analysis to randomize their values based on potential cracks and imperfections in each material sample. The Ψ factors were based on the wave type (shear, transverse, longitudinal), frequency (real life effects of high frequency are not built into v_max model), flaws, ductile and brittle failure, and fatigue failure. We then solved for the velocity at which failure is guaranteed from the material-defined value v_max to a limiting particle velocity, v_lim for the j^th material sample (created about 10,000 samples per raw material). In other words, for a particular case defined by the type of acoustic wave and the shape of the structure that carries it, v_lim (not v_max) defines the threshold between material integrity and failure. The Ψ equations are shown below.

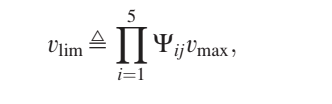
Solving for v_lim as a function of v_max and Ψ₁ – Ψ₅ (left)

Using MATLAB, I simulated tens of thousands of random material “samples” for the 11 materials we had chosen as a baseline for our Monte Carlo model. Each individual sample (sample j) of material X was assigned a v_lim value that was based on the material’s v_max and the j^th sample’s Ψ₁ – Ψ₅ values.

What we found across the board was the likelihood in a random sample of any material, including diamond, was around 50% or greater around 1 ^m/_s threshold in all 11 materials (within 1 order of magnitude). What’s interesting about diamond is that despite its high theoretical v_max limit, the effects of imperfections and stress concentrations were stronger on diamond that any other material on our list, which is why the likelihood of failure in diamond is still 50% at 3 ^m/_s as shown in below.

Velocity at probability of failure (P_f) of 50%, plot maximum particle velocity in a solid wave (v_lim) versus the probability of failure (P_f) for all 11 materials (right)

Project outcome

Since I was only able to work on this project for two quarters with Professor Friend, I was only able to establish the main Monte Carlo model that would later be used to solve for the probability of 50% failure (P_f = 50%) of each of the 11 materials we had selected. When I graduated, I handed off my MATLAB model to Professor Friend’s graduate student, Naiqing Zhang. Naiqing spent the next year working with Professor Friend on the graphs, presentation, and structure of the paper. He also added a section about the immediate relevance of our discovery in the world of acoustofluidics and helped Professor Friend with the theoretical derivation in the appendix.

About two years after I graduated, Professor Friend called me to congratulate me on the work I did years earlier to get this paper published. Professor Friend and Naiqing were able to leverage their acoustofluidics contacts at the the Journal of the Acoustical Society of America (JASA) to get the paper published, and the project was a resounding success.

ARIK SINGH